On teaching an undergraduate course

- Course Website: SYDE 312
Context: As a first year P.hD student at the University of Waterloo, I was given the opportunity to instruct ‘SYDE 312: Applied Linear Algebra’ for a cohort of 84 students during Winter 2025. This post is a reflection of my experiences as an instructor, outlining the lessons I learned and my thoughts on teaching.
A week before christmas in 2024, I was having a candid conversation with my former co-supervisor Prof. John Zelek on research and pedagogy. I casually remarked “As far as my retrospection goes, teaching has always been an enjoyable experience for me. To understand things deeply, I focus on trying to explain them well. Infact, I personally feel that I grasp better when I learn with the intention to teach”. Prof. Zelek, after some quiet consideration, replied “Well then, you might be lucky. We need an instructor for a third year applied linear alegbra course in SYDE. Would you be interested?”.
This was an excellent opportunity for me, considering that – (a) Ever since a young age, I always enjoyed teaching (I read Feynman’s “Six Easy Pieces” in high school and became fascinated by how well he broke down complex topics into simple explanations), and (b) For a while, I’ve been wanting to re-learn linear algebra from the fundamentals, especially from the perspective of machine learning. So, without any second thoughts, I readily expressed my willingness.
In the following three months, I gained invaluable experience as a first-time instructor at a top-ranking institution: from planning the course structure to coordinating administrative tasks to brainstorming new ideas to keep my class interested, engaged, and curious to learn math, it was quite the learning curve for me. This post is an attempt to record my thoughts and experiences on the same.
In my view, teaching encompasses three major parts: (i) Learning (preparation, review, fact-checks, mental notes), (ii) Imparting (lecture delivery, engagement, solving queries), and (iii) Administration (planning, scheduling, coordination, grading). Below are some elaborations on each of these and my thoughts on the same:
–> Add a Venn diagram showing the intersection of these three.
The Learning Part
Learning is time-constrained. Learning the course content (especially for the first-time) is a demanding task where you have to re-structure your everyday life around it. Hitherto, whenever I felt stressed or burned out from prolonged periods of learning, I used to pursue other leisurely activities and resume back after a couple of well-rested days. But, learning for teaching is a heavily time-constrained activity; there’s limited flexibility to cancel or postpone a class because you didn’t have the ‘mood’ to prepare. This made me re-evaluate and re-adjust my learning efficiency to be in sync with my bi-weekly lectures. I had to find the right balance between efforts and exhaustion to be consistent.
Anticipate potential questions. Once I finished reviewing a topic, I developed the habit of noting down relevant questions that might arise, especially when it was abstract, ambiguous, or complicated. This helped me anticipate potential questions from students and prepare beforehand. Needless to say, this greatly improved the quality of my lecture too. There were times when, despite comprehensive preparation, I was thrown completely off-guard; but, I always made sure to try my best to answer ad-hoc questions during class and follow-up with a more detailed explanation post class hours. The latter habit gave me enough time to think, reflect, refer, and answer - it actually helped me gained a deeper understanding of the concepts too. Win-Win!
Structuring course content. I revamped the entire course structure compared to the previous iteration and prepared my lectures from scratch to suit my teaching style and philosophy. Restructuring a course is a two-step process: planning the macro-structure to decide gradable deliverables and topics to cover each week, and planning the micro-structure to decide the hour-wise topic split, slide length, medium of explanation (slide vs. blackboard) and so forth. Albeit creative, it is heavily time-consuming too.
To give an example, when I was preparing lecture slides for basis vectors, I was compelled to include the closely related concept of change of basis. But, since the latter required more fundamental knowledge of linear maps and vector space geometry, I had to overcome the urge and push it to a later week. The important thing to note here is that, this decision took me a good few hours to make. This, again, was a balancing act between quantity and quality.
Generally speaking, learning for teaching is a laborious but serendipitous process, that demands the required efforts out of you. But, the end result is an excellent understanding and unparalleled mastery of concepts with a long retention span. That’s worth all the efforts, isn’t it?
The Imparting Part
Being explicit about my requirements. From the very first day of classes, I made it clear that all tests will be an evaluation of understanding, not memory. Oftimes, in math courses, one tends to overfit to definitions/formulas via rote learning, without developing an intuition for its meaning. In my opinion, this is an absolute waste of efforts, time, and energy, leading to a temporary superficial confidence (first peak of Duning-Kruger curve) at the cost of deeper comprehension. Therefore, I took the assiduous approach of explaining things in great detail, sometimes investing more than my pre-planned time (and efforts). But, in the end, it worked wonders - the final class average stood at 83%, a remarkable ~15% increase compared to the previous iteration. The biggest lesson here is that grades follow understanding and not the other way around.
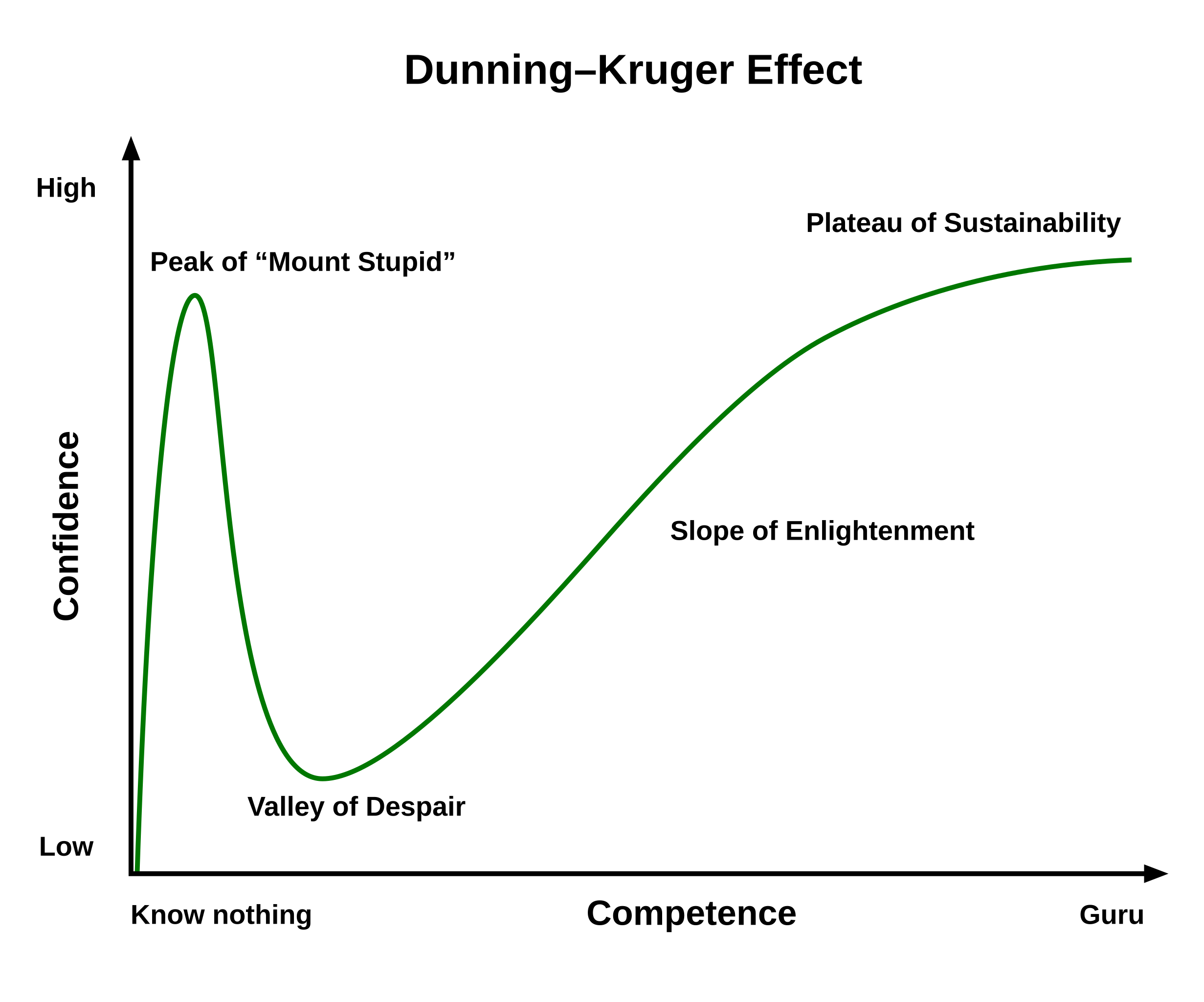
Intuition over definitions. I devoted a lot of time in my course in explaining the intuition behind concepts. For example, while learning about eigenvalues and eigenvectors, most of us would have come across the formulae Av = λv, but only some of us know its essence: it talks about a linear transformation that strecthes/squishes a vector v without knocking it off from its original span. This makes abstract mathematical symbols make more sense, and therefore, helps solidify our understanding. My driving philosophy here was to be the teacher I wish I had in my undergrad.
Food for thought. Every week, at the end of my lecture, I introduced a brain-teaser like the prisonner’s dilemma or the birthday problem, just to encourage everyone to have fun while solving problems. Most often, these topics were not based on linear algebra, but required common sense and logical thinking. This helped blow off steam after a long (2-hour) lecture and often led to lively discussions. I considered this as a thought-provoking exercise that helped bond with my students.
Fostering open discussions and feedback loops.
Encouraging efforts over results.
Administrative tasks.
- Final project encouragement.
- Flexibility with submissions.
Sidenote: Staying healthy. Although this might sound clichéd, the limited flexibility in my schedule made me recognize the importance of both my physical and mental health. I prioritized practicing meditation and hitting the gym everyday. If I was busy with an important task or didn’t have the motivation, I made sure to go on a long walk. I cut down on eating outside and took time to cook during the weekend for the entire week. This helped me immensely with staying in good physical shape and remain mentally sharp, day-in and day-out. I cannot stress this point enough.
I hope this helps you in your teaching journey. Best of luck!
Resources:
Coursework:
- I extensively referred to Sheldon Axler’s Linear Algebra Done Right textbook for most of the topics in this course. He has written clear-cut definitions and explanations.
- For intuition and visualization, I referred to Grant Sanderson’s 3B1B linear Algebra series in youtube. If you haven’t watched his videos, I would highly recommend watching it.
- For selected topics like change of bases and practical applications, I referred to David Lay’s Linear Algebra and its applications textbook.
Templates:
Slide template: Assignment and report template: